Cryptographic Key Generation Using Handwritten Signature
Posted : admin On 23.05.2020- An offline signature-based fuzzy vault (OSFV) is a bio-cryptographic implementation that uses handwritten signature images as biometrics instead of traditional passwords to secure private.
- Apr 17, 2006 Cryptographic key generation using handwritten signature Our signature-based key generation scheme implements the cryptographic construction named fuzzy vault. The use of distinctive signature features suited for the fuzzy vault is discussed and evaluated.
- Based on recent works showing the feasibility of key generation using biometrics, we study the application of handwritten signature to cryptography. Our signature-based key generation scheme implements the cryptographic construction named fuzzy vault. The use of distinctive signature features suited for the fuzzy vault is discussed and evaluated.
- Cryptographic Signatures.; 3 minutes to read +9; In this article. Cryptographic digital signatures use public key algorithms to provide data integrity. When you sign data with a digital signature, someone else can verify the signature, and can prove that the data originated from you and was not altered after you signed it.
- The cryptographic key that the sending party uses to encipher the data must be available to the receiving party to decipher the data. Figure 1 is a simplified illustration of the cryptographic components that are needed to encipher and decipher data in a secret key cryptographic system. In this system, Tom and Linda have established a secure.
- It is Digital signatures are the public-key primitives of message authentication in cryptography. In fact, in the physical world, it is common to use handwritten signatures on handwritten or typed messages at this time. Mainly, they are used to bind signatory to the message to secure the message.
- Cryptographic Key Generation Using Handwritten Signature Software
- Cryptographic Key Generation Using Handwritten Signature Software
- Cryptographic Key Generation Using Handwritten Signature Form
- Cryptographic Key Generation Using Handwritten Signature Template
A digital signature is a mathematical scheme for verifying the authenticity of digital messages or documents. A valid digital signature, where the prerequisites are satisfied, gives a recipient very strong reason to believe that the message was created by a known sender (authentication), and that the message was not altered in transit.
Fuzzy commitment scheme for generation of cryptographic keys based on iris biometrics
Fuzzy commitment scheme for generation of cryptographic keys based on iris biometrics
Cisco crypto key generate ec. For access to this article, please select a purchase option:
Buy article PDF
Buy Knowledge Pack
IET members benefit from discounts to all IET publications and free access to E&T Magazine. If you are an IET member, log in to your account and the discounts will automatically be applied.
Cryptographic Key Generation Using Handwritten Signature Software
 Recommend Title Publication to library
Recommend Title Publication to libraryThank you
Your recommendation has been sent to your librarian.
This work presents a method based on information-theoretic analysis of iris biometric that aims to extract homogeneous regions of high entropy. Successful extraction of these regions facilitates the development of effective systems for generation of cryptographic keys of lengths up to 400 bits per iris. At the same time, this approach allows for the application of simpler error correction codes with equal false accept rate levels, which reduces the overall complexity of this class of systems.
Cryptographic Key Generation Using Handwritten Signature Software
References
- 1)
- 1. Soutar, C., Roberge, D., Stoianov, A., et al: ‘Biometric encryption’, in Nichols, R.K. (ed.): ‘ICSA guide to cryptography’ (McGraw-Hill Publishers, New York, 1999).
- 2)
- 2. Davida, G.I., Frankel, Y., Matt., B.J., et al: ‘On the relation of error correction and cryptography to an offline biometric based identification scheme’. In Proceedings of WCC99, Workshop on Coding and Cryptography, 1999.
- 3)
- 3. Hao, F., Anderson, R., Daugman, J.: ‘Combining crypto with biometrics effectively’, IEEE Trans. Comput., 2006, 55, (9), pp. 1081–1088.
- 4)
- 4. Kanade, S., Camara, D., Krichen, E., Petrovska-Delacretaz, D., Dorizzi, B., et al: ‘Three factor scheme for biometric-based cryptographic key regeneration using iris,’ in The 6th Biometrics Symposium 2008 (BSYM2008), September 2008.
- 5)
- 5. Garcia-Baleon, H.A., Alarcon-Aquino, V., Starostenko, O., et al: ‘Bimodal biometric system for cryptographic key generation using wavelet’. IEEE Mexican Int. Conf. on Computer Science, 2009, pp. 186–196.
- 6)
- 6. Hao, F., Chan, C.W.: ‘Private key generation from on-line handwritten signatures’, Inf. Manag. Comput. Sec., 2002, 10, (2), pp. 159–164.
- 7)
- 7. Tuyls, P., Akkermans, A.H.M., Kevenaar, T.A.M., et al: ‘Practical biometric authentication with template protection’. Proc. of the 5th Int. Conf. on Audio- and Video-Based Biometric Person Authentication, AVBPA'05, 2005, pp. 436–446.
- 8)
- 8. van der Veen, M., Kevenaar, T., Schrijen, G.-J., et al: ‘Face biometrics with renewable templates’. Proc. SPIE 6072, Security, Steganography, and Watermarking of Multimedia Contents VIII, 60720J, February 2006.
- 9)
- 9. Monrose, F., Reiter, M.K., Li, Q., et al: ‘Cryptographic key generation from voice’. Proc. of the 2001 IEEE Symp. on Security and Privacy, May 2001.
- 10)
- 10. Clancy, T.C., Kiyavash, N., Lin, D.J.: ‘Secure smart card-based fingerprint authentication’. Proc. ACM SIGMM Workshop Biometrics Methods and Application (WBMA), 2003.
- 11)
- 11. Rathgeb, C., Uhl, A.: ‘Two-factor authentication or how to potentially counterfeit experimental results in biometric systems’. Proc. of the Int. Conf. on Image Analysis and Recognition, 2010, pp. 296–305.
- 12)
- 12. Daugman, J.: ‘The importance of being random’, Stat. Princ. Iris Recognit., Pattern Recognit., 2003, 36, (2), pp. 279–291.
- 13)
- 13. Bringer, J., Chabanne, H., Cohen, G., Kindarji, B., Zemor, G., et al: ‘Theoretical and practical boundaries of binary secure sketches’, IEEE Trans. Inf. Forensics Sec., 20083, (4), pp. 673–683.
- 14)
- 14. Kelkboom, E.J.C., Breebaart, J., Kevenaar, T.A.M., et al: ‘Preventing the decodability attack based cross-matching in a fuzzy commitment scheme’, IEEE Trans. Inf. Forensics Sec., 2011, pp. 107–121.
- 15)
- 15. Rathgeb, C., Uhl, A.: ‘Statistical attack against fuzzy commitment scheme’, IET Biometrics, 2012, pp. 94–104.
- 16)
- 16. Maiorana, E., Campisi, P., Neri, A.: ‘IRIS template protection using a digital modulation paradigm’. 2014 IEEE Int. Conf. on Acoustics, Speech and Signal Processing (ICASSP), Florence, 2014, pp. 3759–3763.
- 17)
- 17. Álvarez Mariño, R., Hernández Álvarez, F., Hernández Encinas, L.: ‘A crypto-biometric scheme based on iris-templates with fuzzy extractors’, Inf. Sci., 2012, 195, pp. 91–102.
- 18)
- 18. Shannon, C.E.: ‘A mathematical theory of communication’, Bell Syst. Techn. J., 1948, 27, pp. 379–423, 623–656.
- 19)
- 19. Shannon, C.E.: ‘Communication theory of secrecy systems’, Bell Syst. Tech. J., 1949, 28, pp. 656–715.
- 20)
- 20. Daugman, J.: ‘How iris recognition works’, IEEE Trans. Circuits Syst. Video Technol., 2004, 14, pp. 21–30.
- 21)
- 21. Gonzalez, R.C., Woods, R.E., Eddins, S.L.: ‘Digital image processing using MATLAB’ (Prentice-Hall, New Jersey, 2003).
- 22)
- 22. Adamovic, S., Milosavljevic, M.: ‘Information analysis of iris biometrics for the needs of cryptology key extraction’, Serb. J. Electr. Eng., 2013, 10, (1), pp. 1–12.
- 23)
- 23. Adamovic, S., Savic, A.G., Milosavljevic, M., et al: ‘Texture analysis of iris biometrics based on adaptive size neighborhood entropy and linear discriminant analysis’. Int. Scientific Conf. – Sinteza, Serbia, April 2014, pp. 658–660.
- 24)
- 24. Masek, L.: ‘Recognition of human iris patterns for biometric identification iris recognition’, http://www.csse.uwa.edu.au/~pk/studentprojects/libor/, accessed 15 October 2012.
- 25)
- 25. Daugman, J.: ‘Uncertainty relation for resolution in space, spatial frequency, and orientation optimized by two-dimensional visual cortical filters’, J. Opt. Soc. Am. A, 1985, 2, (7), pp. 1160–1169.
- 26)
- 26. Juels, A., Wattenberg, M.: ‘A fuzzy commitment scheme’. Proc. of the 6th ACM Conf. on Computer and Communications Security, 1999.
- 27)
- 27. Biometrics Ideal Test, http://biometrics.idealtest.org, accessed 15 October 2013.
- 28)
- 28. Goh, A., Ngo, D.C.L.: ‘Computation of cryptographic keys from face biometrics. communications and multimedia security’. ‘Advanced techniques for network and data protection’ (Springer Berlin Heidelberg, 2003), pp. 1–13.
- 29)
- 29. Zhou, X., Kuijper, A., Veldhuis, R., et al: ‘Quantifying privacy and security of biometric fuzzy commitment’. Biometrics (IJCB), 2011 Int. Joint Conf. on, Washington, DC, 2011, pp. 1–8.
- 1)
Related content
Cryptographic digital signatures use public key algorithms to provide data integrity. When you sign data with a digital signature, someone else can verify the signature, and can prove that the data originated from you and was not altered after you signed it. For more information about digital signatures, see Cryptographic Services.
This topic explains how to generate and verify digital signatures using classes in the System.Security.Cryptography namespace.
Generating Signatures
Digital signatures are usually applied to hash values that represent larger data. The following example applies a digital signature to a hash value. First, a new instance of the RSACryptoServiceProvider class is created to generate a public/private key pair. Next, the RSACryptoServiceProvider is passed to a new instance of the RSAPKCS1SignatureFormatter class. This transfers the private key to the RSAPKCS1SignatureFormatter, which actually performs the digital signing. Before you can sign the hash code, you must specify a hash algorithm to use. This example uses the SHA1 algorithm. Finally, the CreateSignature method is called to perform the signing.
Due to collision problems with SHA1, Microsoft recommends SHA256 or better.
Signing XML Files
The .NET Framework provides the System.Security.Cryptography.Xml namespace, which enables you sign XML. Signing XML is important when you want to verify that the XML originates from a certain source. For example, if you are using a stock quote service that uses XML, you can verify the source of the XML if it is signed.
The classes in this namespace follow the XML-Signature Syntax and Processing recommendation from the World Wide Web Consortium.
Verifying Signatures
To verify that data was signed by a particular party, you must have the following information:
This group of websites is your competition. You should take some time to look into the patterns involved with how people search. Then you will have a better chance of finding keywords that will truly attract their attention.After you have developed a few keywords you are interested in targeting, plug them into the search engines and see what comes up. Then add these pieces to strategic locations throughout your website for maximum exposure.Step 5: Rinse and Repeat!Remember, it’s going to take some practice if you really want to get good at creating keyword rich content. Generate key word from content list. Plus, focus on building content that incorporates the most popular keywords that you have found.
The public key of the party that signed the data.
The digital signature.
The data that was signed.
The hash algorithm used by the signer.
Cryptographic Key Generation Using Handwritten Signature Form
To verify a signature signed by the RSAPKCS1SignatureFormatter class, use the RSAPKCS1SignatureDeformatter class. The RSAPKCS1SignatureDeformatter class must be supplied the public key of the signer. You will need the values of the modulus and the exponent to specify the public key. (The party that generated the public/private key pair should provide these values.) First create an RSACryptoServiceProvider object to hold the public key that will verify the signature, and then initialize an RSAParameters structure to the modulus and exponent values that specify the public key.
The following code shows the creation of an RSAParameters structure. The Modulus property is set to the value of a byte array called modulusData and the Exponent property is set to the value of a byte array called exponentData.
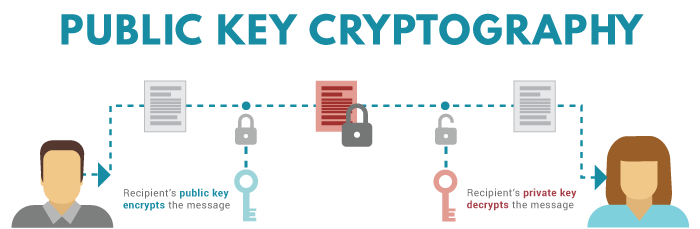
After you have created the RSAParameters object, you can initialize a new instance of the RSACryptoServiceProvider class to the values specified in RSAParameters. The RSACryptoServiceProvider is, in turn, passed to the constructor of an RSAPKCS1SignatureDeformatter to transfer the key.
The following example illustrates this process. In this example, hashValue and signedHashValue are arrays of bytes provided by a remote party. The remote party has signed the hashValue using the SHA1 algorithm, producing the digital signature signedHashValue. The RSAPKCS1SignatureDeformatter.VerifySignature method verifies that the digital signature is valid and was used to sign the hashValue.
This code fragment will display 'The signature is valid' if the signature is valid and 'The signature is not valid' if it is not.